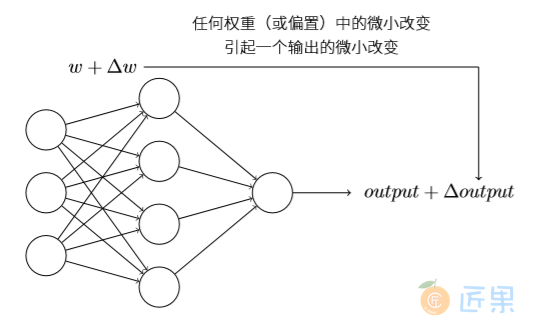
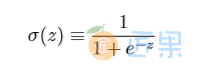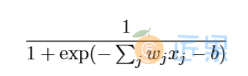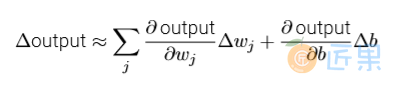学习算法听上去⾮常棒。但是我们怎样给⼀个神经⽹络设计这样的算法呢？假设我们有⼀个感知器⽹络，想要⽤它来解决⼀些问题。例如，⽹络的输⼊可以是⼀幅⼿写数字的扫描图像。我们想要⽹络能学习权重和偏置，这样⽹络的输出能正确分类这些数字。为了看清学习是怎样⼯作 的，假设我们把⽹络中的权重（或者偏置）做些微⼩的改动。就像我们⻢上会看到的，这⼀属性会让学习变得可能。这⾥简要⽰意我们想要的（很明显这个⽹络对于⼿写识别还是太简单了！）

如果对权重（或者偏置）的微⼩的改动真的能够仅仅引起输出的微⼩变化，那我们可以利⽤这⼀事实来修改权重和偏置，让我们的⽹络能够表现得像我们想要的那样。例如，假设⽹络错 误地把⼀个“9”的图像分类为“8”。我们能够计算出怎么对权重和偏置做些⼩的改动，这样⽹络能够接近于把图像分类为“9”。然后我们要重复这个⼯作，反复改动权重和偏置来产⽣更好 的输出。这时⽹络就在学习。

问题在于当我们的⽹络包含感知器时这不会发⽣。实际上，⽹络中单个感知器上⼀个权重或 偏置的微⼩改动有时候会引起那个感知器的输出完全翻转，如0变到1。那样的翻转可能接下来引起其余⽹络的⾏为以极其复杂的⽅式完全改变。因此，虽然你的“9”可能被正确分类，⽹络在其它图像上的⾏为很可能以⼀些很难控制的⽅式被完全改变。这使得逐步修改权重和偏置来让⽹络接近期望⾏为变得困难。也许有其它聪明的⽅式来解决这个问题。但是这不是显⽽易⻅地能让⼀个感知器⽹络去学习。

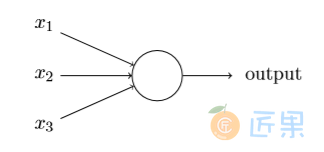
我们可以引⼊⼀种称为S型神经元的新的⼈⼯神经元来克服这个问题。S型神经元和感知器 类似，但是被修改为权重和偏置的微⼩改动只引起输出的微⼩变化。这对于让神经元⽹络学习起来是很关键的。 好了，让我来描述下S型神经元。我们⽤描绘感知器的相同⽅式来描绘S型神经元：

正如⼀个感知器，S型神经元有多个输⼊，x1,x2,...。但是这些输⼊可以取0和1中的任意 值，⽽不仅仅是0或1。例如，0.638...是⼀个S型神经元的有效输⼊。同样，S型神经元对每个输⼊有权重，w1,w2,...，和⼀个总的偏置，b。但是输出不是0或1。相反，它现在是 σ(w·x+b)， 这⾥σ被称为S型函数，定义为：

把它们放在⼀起来更清楚地说明，⼀个具有输⼊x1,x2,...，权重w1,w2,...，和偏置b的S 型神经元的输出是：

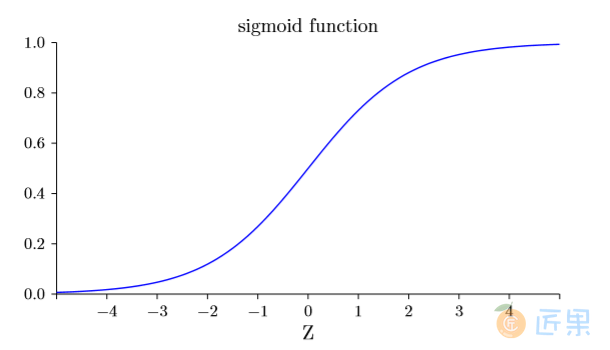
初看上去， S型神经元和感知器有很⼤的差别。如果你不熟悉S型函数的代数形式，它看上去晦涩难懂⼜令⼈⽣畏。实际上，感知器和S型神经元之间有很多相似的地⽅，跨过理解上的障碍，S型函数的代数形式具有很多技术细节。

为了理解和感知器模型的相似性，假设 z ≡ w ·x + b 是⼀个很⼤的正数。那么 e−z ≈ 0 ⽽ σ(z) ≈ 1。即，当 z = w·x + b 很⼤并且为正，S型神经元的输出近似为1，正好和感知器⼀样。 相反地，假设 z = w·x + b 是⼀个很⼤的负数。那么 e−z →∞，σ(z) ≈ 0。所以当 z = w·x + b 是⼀个很⼤的负数，S型神经元的⾏为也⾮常近似⼀个感知器。只有在 w·x+b 取中间值时，和感知器模型有⽐较⼤的偏离。

σ的代数形式⼜是什么？我们怎样去理解它呢？实际上，σ的精确形式不重要——重要的是这个函数绘制的形状。是这样：

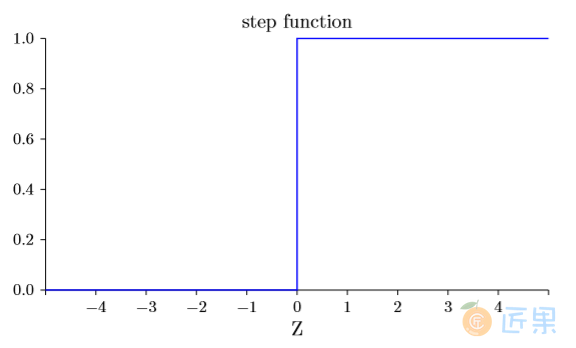
这个形状是阶跃函数平滑后的版本：

如果σ实际是个阶跃函数，既然输出会依赖于 w·x + b 是正数还是负数，那么S型神经元 会成为⼀个感知器。利⽤实际的σ函数，我们得到⼀个，就像上⾯说明的，平滑的感知器。的确，σ函数的平滑特性，正是关键因素，⽽不是其细部形式。σ的平滑意味着权重和偏置的微⼩ 变化，即 ∆wj 和 ∆b ，会从神经元产⽣⼀个微⼩的输出变化 ∆output。实际上，微积分告诉我们 ∆output 可以很好地近似表⽰为：

其中求和是在所有权重wj上进⾏的，⽽ ∂output/∂wj 和 ∂output/∂b 符号表⽰output分别对于 wj 和b的偏导数。如果你对偏导数感到不⾃在，不⽤惊慌。上⾯全部⽤偏导数的表达式看上去很复杂，实际上它的意思⾮常简单（这可是个好消息）：∆output 是⼀个反映权重和偏置变 化——即 ∆wj 和 ∆b ——的线性函数。这⼀线性使得选择权重和偏置的微⼩变化来达到输出的微⼩变化的运算变得容易。所以当S型神经元有更多和感知器相同的本质的⾏为时，计算如何变化权重和偏置来使输出变化会更加容易。

如果对σ来说重要的是形状⽽不是精确的形式，那为什么要在公式（3）中给σ使⽤特定的形式呢？实际上，在这本书的后⾯我们会碰巧考虑到为其它激活函数 f(·) 输出为 f(w·x + b) 的神 经元。当我们使⽤⼀个不同的激活函数，最⼤的变化是公式(5)中⽤于偏导数的特定值的改变。 事实证明当我们后⾯计算这些偏导数，⽤σ会简化数学计算，这是因为指数在求导时有些可爱 的属性。⽆论如何，σ在神经⽹络的⼯作中被普遍使⽤，并且是这本书中我们最常使⽤的激活函 数。

我们应该如何解释⼀个S型神经元的输出呢？很明显，感知器和S型神经元之间⼀个很⼤的 不同是S型神经元不仅仅输出0或1。它可以输出0和1之间的任何实数，所以诸如0.173...和 0.689...的值是合理的输出。这是⾮常有⽤的，例如，当我们想要输出来表⽰⼀个神经⽹络的图 像像素输⼊的平均强度。但有时候这会是个⿇烦。假设我们希望⽹络的输出表⽰“输⼊图像是 ⼀个9”或“输⼊图像不是⼀个9”。很明显，如果输出是0或1是最简单的，就像⽤感知器。但是在实践中，我们可以设定⼀个约定来解决这个问题，例如，约定任何⾄少为0.5的输出为表⽰“这是⼀个9”，⽽其它⼩于0.5的输出为表⽰“不是⼀个9”。当我们正在使⽤这样的约定时，我 总会清楚地提出来，这样就不会引起混淆。